
數(shù)學(xué)科學(xué)學(xué)微分方程團(tuán)隊(duì)周立群教授近日在IEEE Transactions on Network Science and Engineering發(fā)表了題為“Global Polynomial Stabilization of Impulsive Neural Networks With Bidirectional Proportional Delays”的學(xué)術(shù)論文。該研究首次提出了一種新的向量形式的時(shí)滯微分不等式方法,應(yīng)用于解決雙向比例時(shí)滯脈沖神經(jīng)網(wǎng)絡(luò)的全局多項(xiàng)式鎮(zhèn)定問題。
脈沖神經(jīng)網(wǎng)絡(luò)的鎮(zhèn)定在優(yōu)化問題中有著廣泛的應(yīng)用。由于網(wǎng)絡(luò)運(yùn)行過程中放大器的開關(guān)和信號(hào)傳輸導(dǎo)致時(shí)滯不可避免。比例時(shí)滯是一類無界時(shí)變時(shí)滯,雙向比例時(shí)滯可更好的刻畫神經(jīng)網(wǎng)絡(luò)的時(shí)滯情況,但是比例時(shí)滯的無界性給神經(jīng)網(wǎng)絡(luò)鎮(zhèn)定研究帶來了很大的挑戰(zhàn)。傳統(tǒng)的構(gòu)造Lyapunov泛函的方法不容易解決向量形式的雙向比例時(shí)滯脈沖神經(jīng)網(wǎng)絡(luò)(BPDINNs)的鎮(zhèn)定問題。為了克服這一困難,周立群教授及其研究團(tuán)隊(duì)通過設(shè)計(jì)易于硬件實(shí)現(xiàn)的反饋控制器,并利用M-矩陣的性質(zhì)構(gòu)造了一個(gè)新的向量形式的時(shí)滯微分不等式。利用提出的時(shí)滯微分不等式、M-錐和M-矩陣的性質(zhì)以及矩陣譜半徑理論,證明了閉環(huán)系統(tǒng)平衡點(diǎn)存在且是唯一。進(jìn)而得到了所研究的BPDINNs的全局多項(xiàng)式鎮(zhèn)定準(zhǔn)則,易于驗(yàn)證。該方法的創(chuàng)新性和優(yōu)點(diǎn)是沒有使用通常的構(gòu)造Lyapunov泛函的研究方法,為雙向比例時(shí)滯脈沖神經(jīng)網(wǎng)絡(luò)的動(dòng)力學(xué)研究提供了新的研究方法及思路。數(shù)值仿真如圖1所示。
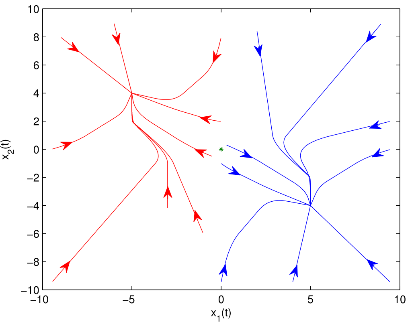
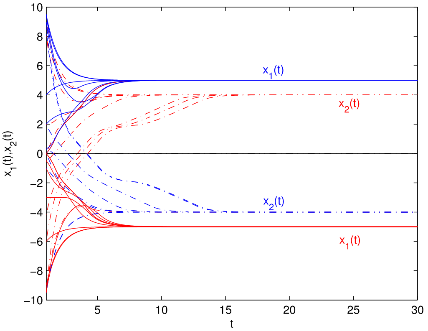
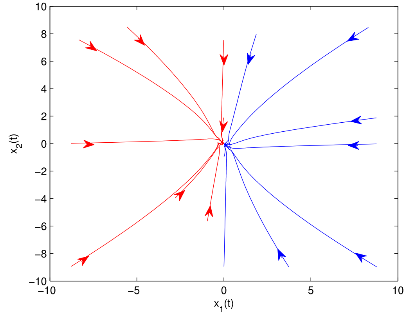
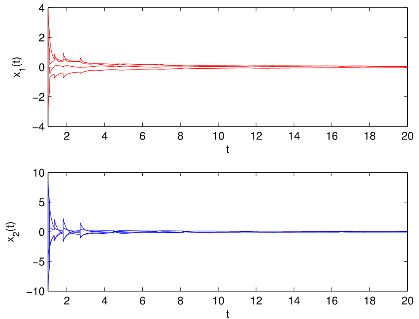
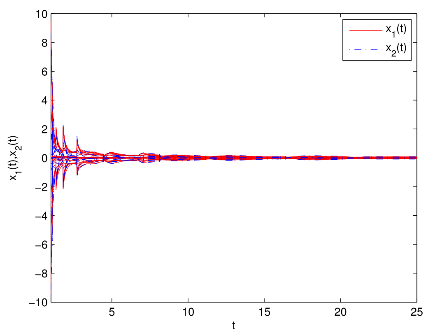
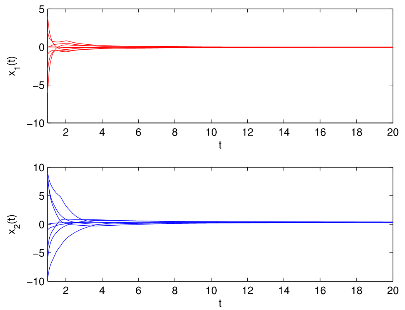
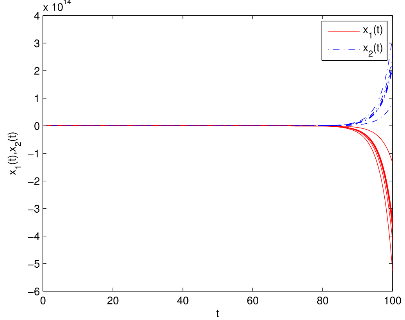
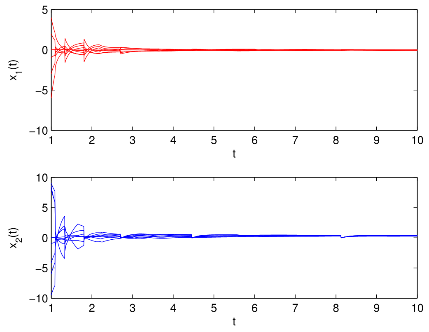
圖1 有/無控制器和有/無脈沖作用時(shí)雙向比例時(shí)滯神經(jīng)網(wǎng)絡(luò)(BPDNNs)的
相圖和時(shí)間響應(yīng)曲線
該工作由天津師范大學(xué)、湖南師范大學(xué)、沈陽(yáng)工業(yè)大學(xué)、Texas A&M的科研人員合作完成。周立群教授為第一作者,湖南師范大學(xué)朱全新教授為通訊作者,天津師范大學(xué)為第一完成單位。該研究獲得國(guó)家自然科學(xué)基金面上項(xiàng)目(11901433、62173139)、天津市自然科學(xué)基金面上項(xiàng)目(18JCYBJC85800)和湖南省科技創(chuàng)新計(jì)劃項(xiàng)目(2021RC4030)的資助。
論文鏈接:https://ieeexplore.ieee.org/document/10198676